Параллелограмм
Параллелогра́мм (бор. грек. παραλληλόγραμμον παράλληλος — параллель һәм γραμμή — һыҙыҡ һүҙҙәренән) — ҡапма-ҡаршы яҡтары параллель, йәғни параллель тура һыҙыҡтарҙа ятҡан дүртмөйөш ул. Тура дүртмөйөш, квадрат һәм ромб параллелограмдың айырым осраҡтары булып торалар.
| Параллелограмм | |
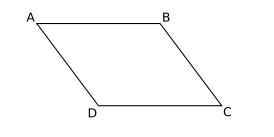 | |
| Грань политопа | ҡабырға[d] |
|---|---|
| Вики-проект | Проект:Математика[d] |

Үҙсәнлектәре
үҙгәртергә- Параллелограмдың ҡаршы ятыусы яҡтары тигеҙ.
- Параллелограмдың ҡаршы ятыусы мөйөштәре тигеҙ.
- Бер яғына теркәлгән мөйөштәренең суммаһы 180°-ҡа тигеҙ (параллель тура һыҙыҡтарҙың үҙсәнлеге буйынса).
- Параллелограмдың диагоналдәре киҫешәләр һәм киҫешеү нөктәһендә урталай бүленәләр:
- .
- Параллелограмдың диагоналдәре киҫешкән нөктә уның симметрия үҙәге була.
- Параллелограмм диагонале менән ике тигеҙ өсмөйөшкә бүленә.
- Параллелограмдың урта һыҙыҡтары уның диагоналдәре киҫешкән нөктәлә киҫешәләр. Был нөктәлә уның ике диагонале һәм ике урта һыҙығы урталай бүленәләр.
- Параллелограмм тождествоһы: параллелограмдың диагоналдәре квадраттарының суммаһы уның ике эргәләш яҡтарының икеләтелгән квадраттары суммаһына тигеҙ: а — AB яғының оҙонлоғо, b — BC яғының оҙонлоғо, һәм — диагоналдәренең оҙонлоҡтары булһын, ти; ул саҡта
- Параллелограмм тождествоһы ирекле дүртмөйөш өсөн Эйлер формулаларының ябай эҙемтәһе булып тора: дүртмөйөштөң диагоналдәренең урталары араһындағы алыҫлыҡтың дүртләтелгән квадраты уның яҡтарының квадраттары суммаһы алынған уның диагоналдәренең квадраттары суммаһына тигеҙ. Параллелограмдың ҡаршы ятыусы яҡтары тигеҙ, ә диагоналдәренең урталары араһындағы алыҫлыҡ нулгә тигеҙ.
- Аффиналы үҙгәртеү һәр ваҡыт параллелограмды параллелограмға күсерә. Теләһә ниндәй параллелограмм өсөн уны квадратҡа үҙгәртеүсе аффиналы үҙгәртеү бар.
Параллелограмдың билдәләре
үҙгәртергәABCD дүртмөйөшө параллелограмм була, әгәр түбәндәге шарттарҙың береһе үтәлһә (был осраҡта бөтә ҡалған шарттар ҙа үтәлә):
- Дүртмөйөштөң ике ҡаршы ятҡан яғы бер үк ваҡытта тигеҙ һәм параллель булһа: .
- Дүртмөйөштөң ҡаршы ятыусы мөйөштәре пар-пар тигеҙ булһа: .
- Дүртмөйөштөң ҡаршы ятыусы яҡтары пар-пар тигеҙ булһа: .
- Дүртмөйөштөң ҡаршы ятыусы яҡтары пар-пар параллель булһа: .
- Диагоналдәре киҫешеү нөктәһендә урталай бүленһәләр: .
- Күрше ятҡан мөйөштәренең суммаһы 180 градус булһа: .
- Ҡабарынҡы дүртмөйөштөң ҡаршы ятыусы яҡтарының урталары араһындағы алыҫлыҡтарҙың суммаһы уның ярым периметрына тигеҙ булһа.
- Ҡабарынҡы дүртмөйөштөң диагоналдәренең квадраттары суммаһы уның яҡтарының квадраттары суммаһына тигеҙ булһа: .
Параллелограмдың майҙаны
үҙгәртергә- Бында тап параллелограммға хас булған формулалар килтерелгән. Шулай уҡ ҡара:
ирекле дүртмөйөштәрҙең майҙандары өсөн формулалар.
Параллелограмдың майҙаны уның нигеҙе менән бейеклеге ҡабатландығына тигеҙ:
- , бында — яғы, — был яғына төшөрөлгән бейеклеге.
Параллелограмдың майҙаны уның яҡтарының улар араһындағы мөйөш синусына ҡабатландығына тигеҙ:
- бында һәм — яҡтары, ә — һәм яҡтары араһындағы мөйөш.
Шулай уҡ параллелограмдың майҙаны яҡтары һәм теләһә ниндәй диагоналенең оҙонлоғо аша Герон формулаһы буйынса ике тигеҙ терәлеп ятҡан өсмөйөштәренең майҙандары суммаһы булараҡ күрһәтелә ала:
- бында
Шулай уҡ ҡара
үҙгәртергәИҫкәрмәләр
үҙгәртергә
Был мәҡәләгә түбәндәгеләр етешмәй. Ошоларҙы төҙәтеп йә өҫтәп, һеҙ уны яҡшырта алаһығыҙ?: |